Help with Excel documents

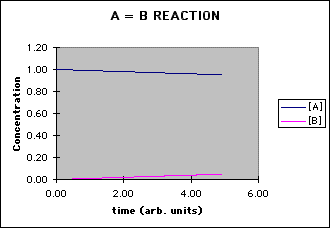
This Microsoft Excel spreadsheet (file AB.xls) uses a primitive differential equation solver to determine the concentration of A and B as a function of time for a simple reaction A = B. The reaction is first order in the forward (A --> B) and reverse direction (B --> A). The parameters that can be adjusted are:

• the initial concentration of A, [A]_o found in cell B2
• the initial concentration of B, [B]_o found in cell C2
• the rate of the forward (A --> B) reaction kAB found in cell D2
• the rate of the reverse (B --> A) reaction kBA found in cell E2

The output of note consists of the:

• initial ratio of B to A, [B]_o /[A]_o found in cell F2
• the final ratio of B to A, found in cell G2
• a graph of [A] and [B] vs. time

The rate constant in the forward (kAB) and the reverse direction (kBA) can be adjusted in the range: 0-6. The initial concentration of A and B should fall in the range 0-1.

The following are suggested conditions that you should investigate.

• Keep kAB = kBA and vary the initial concentrations of [A]_o and [B]_o to determine how these initial concentrations affect the final ratio, [B]/[A] and the time it takes to achieve this ratio.
• Keep [A]_o and [B]_o constant and vary kAB and kBA to determine how these changes affect the final ratio, [B]/[A] and the time it takes to achieve this ratio.
• Vary the rate constants and initial concentrations and try to determine some general rules for predicting the final [B]/[A] ratio and the time it takes to achieve this ratio.